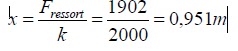CHAPITRE 1
F atteint une valeur maximale de 2 kN , que la constante dukN/m et que le coefficient de frottement entre la masse et le plan est 0,1 ; àLa distance
F ne peut pas partir de zéro. En effet, la force deF varie de m g fg = 98 N à 2 kN
L’énergie accumulée dans le ressort est
F est enlevée, quelle sera la vitesse maximaleM = 100 kg si le coefficient de frottement entre la masse et let = 0 et x = 0, le ressort est étiré et la masse est en B’. L’énergie dans le ressortN·m et la force est 1902 N. En présence de frottement, le force sur laN à 98 N durant la glissade, soit une valeur moyenne deN.F=m a, l’accélération moyenne de la masse de 100 kg, durant la glissade, seraa moy = 853/100 = 8,53 m/s2.a durant la glissadeamoy.
Pour un mouvement uniformément accéléré, on a :
kN·m.kN·m.
x dont se sera étiré le ressort est :
1.1 À la figure 1.1 (dans le texte), si la force externe
en position B’
F est enlevée lorsque la masse est, à quelle extrémité de la corde se trouve alors son entrée?Réponse : A’. Le ressort est alors tendu et il ramène la masse vers la position B.
L’inertie de la masse est la charge et la traction du ressort est la force motrice, l’entrée.
1.2 On suppose que la force
ressort est 2
L’énergie accumulée dans le ressort est
Pour que ce système fonctionne, la force
frottement exige que la force 
1.3 En absence de frottement, toute l’énergie emmagasinée dans le ressort est
transférée à la masse en énergie cinétique. En absence de frottement, l’énergie
emmagasinée dans le ressort est de 2 1.3 En absence de frottement, toute l’énergie emmagasinée dans le ressort est
transférée à la masse en énergie cinétique. En absence de frottement, l’énergie
emmagasinée dans le ressort est de 2 1.4 À la figure 1.1, si la force externe
atteinte par la masse
plan vaut 0,1? À quelle distance et après combien de temps, à partir du début du
mouvement, cette valeur sera-t-elle atteinte?
À
est 904,4
masse va varier de (1902 -98)
853 De
donc,
Pour simplifier le problème, on va supposer que l’accélération
est constante et égale à
Alors, on peut écrire que l’énergie cinétique de la masse à la fin la glissade est :
Le travail fait par la force de frottement durant ce temps est :
W m g f x
f g =À la fin la glissade, la somme de l’énergie cinétique de la masse et du travail fait par la
force de frottement doit être égale à l’énergie élastique emmagasinée dans le ressort au
début du mouvement, soit :En notant que
temps de la glissade
force de frottement durant le temps
fait par la force de frottement et l’énergie cinétique de la masse vaut bien l’énergie
élastique disponible dans le ressort au début.v0 = 0 et en solutionnant, on trouve Ekmasse = 811,2 N·m, v = 4,02 m/s, let = 0,471 s et la distance glissée x = 0,947 m. Le travail fait par lat sur la distance x vaut 92,8 N·m ; la somme du travail kN·m.kN·m.
