Un joint universel ne produit pas un mouvement de sortie constant, sauf si l’angle
n'est pas le cas évidemment quand on utilise un joint universel. On peut cependant remédier à la
situation en combinant plusieurs joints en série et faire en sorte que les erreurs des uns compensent
celles des autres. On obtient alors un mouvement de sortie uniforme avec des fluctuations dans les
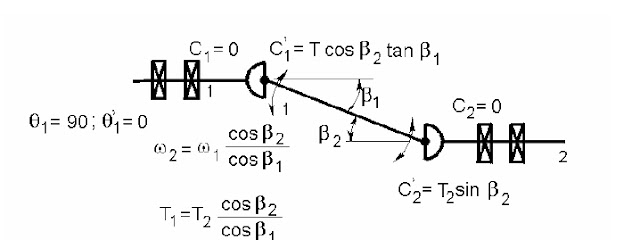
pièces intermédiaires. Un tel arrangement est montré à la figure 10.22. Cette figure montre qu’un
arbre intermédiaire, 1', a été ajouté entre l’arbre d’entrée et celui de sortie. Cet arbre porte à chacune
de ses extrémités la fourchette d’un joint. L’angle total
se trouve ainsi partagé en deux angles
règles précises doivent être respectées pour obtenir cette annulation des erreurs Figure 10.22 - Représentation d'un arrangement de deux joints universels avec tous les arbres dans
le même plan et les fourchettes de l'arbre intermédiaire en phaseLes différents cas qui peuvent se présenter sont les suivants :
1. L’arbre d’entrée, 1, l’arbre de sortie, 2, et l’arbre intermédiaire, 1', sont tous situés dans un même
plan ou dans des plans différents contenant chacun les arbres 1 et 1' et 1' et 2.
2. Les angles
3. Les fourchettes aux extrémités de l’arbre intermédiaire sont situées chacune simultanément dans
le plan de leur joint respectif ou dans un plan perpendiculaire, à tous les 90
arbres. On dit alors qu’elles sont en phase. Si cette situation n’est pas réalisée, elles sont alors
déphasées.
Considérons par exemple un arrangement comme celui de la figure 10.22 avec tous les arbres dans
un même plan et les fourchettes de l’arbre intermédiaire en phase. Dans la figure 10.22a, l’arbre 1
entraîne l’arbre 1' et l’angle
β1 et β2 des joints sont égaux ou différents.o de rotation desθ1 vaut 90o. Dans ces conditions, on sait par l’équation (10.10) queω
ici par suite de l’équation (10.9) que
trouve :Si
couples À partir de ceci, on peut déduire les conditions nécessaires et suffisantes pour qu’un arrangement de
deux joints universels transmette un mouvement uniforme1. Il faut que
2. Les fourchettes de l’arbre intermédiaire doivent être en phase.
Si ces deux conditions sont respectées, que tous les arbres soient dans un même plan ou non,
l’ensemble des deux joints transmet un mouvement uniforme entre l’entrée et la sortie. Les pièces
intermédiaires subissent cependant des accélérations et des décélérations deux fois par tour.
Si
deux joints se comporte alors comme un joint simple dont l’angle L’angle
l’arbre d’entrée avec l’équation (10.15).
Si les deux fourchettes de l’arbre intermédiaire ne sont pas en phase, l’angle
relation :où
phase, alors le calcul est plus complexe (voir réf. β1 n’est pas nécessairement égal à β2. Si les fourchettes sont partiellement en phase ou horsβéqui est utile pour calculer l’accélération α et le retard ou l’avance de l’arbre de sortie surβéqui se calcule par laβ1 = β2.β1 est différent de β2, alors les fourchettes de l’arbre intermédiaire sont en phase. Le montage desβéqui se calcule parβ2 = β1, on retrouve ω2 = ω1 comme désiré. Si on fait un raisonnement semblable avec lesT1 et T2, on trouve alors :'1 = ω1/cos β1. À son tour, l’arbre 1' entraîne l’arbre 2 avec l’angle θ'’1 = 0o. On peut donc écrireω2 = ω'1 cos β2. En combinant ces deux expressions, onβ est nul, ce quiβ du joint entre l’arbre d’entrée et de sortieβ1 et β2 entre les deux joints 1 et 2. Cependant, certaines