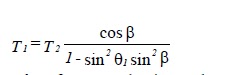La fonction première d’un joint universel est d’entraîner deux arbres ayant un décalage angulaire de
β >
pour un angle de rotation
0o. Dans ce cas, l’arbre entraîné n’est pas toujours en phase avec l’arbre moteur, c'est-à-dire queθ1 entre 0o et 90o de l’arbre moteur, l’arbre entraîné tourne d’un angle θ2plus petit que
de suite.
La figure 10.21a représente le joint universel de la figure 10.18 avec la convention définie à la figure
10.20. La figure 10.21b est la projection du joint de la figure 10.21a dans un plan normal à l’arbre
d’entrée.Figure 10.21 - Étude cinématique du joint universel
Dans le plan de projection, les extrémités B et C de la croix qui sont dans la fourchette de l’arbre
d’entrée décrivent un cercle de rayon les extrémités D et E de la croix qui sont dans la fourchette de l’arbre de sortie décrivent une ellipse
dans le même plan de projection.
Pour un angle de rotation
l’arbre d’entrée se trouve en B' sur le cercle (figure 10.21b). Dans cette rotation de
de la croix dans la fourchette de l’arbre de sortie se retrouve en D' sur l’ellipse. Le point D' est
localisé sur l’ellipse en sachant que l’angle droit des bras de la croix, l’angle
toujours comme un angle droit, de sorte queBOB’ =∠ DOD’ =θ1Pour trouver l’angle
L’angle
Dans les triangles Or, comme
tan En général, en transmission de puissance, la vitesse d’entrée
sortie
supposant où
d’entrée mesuré à partir de la position où la fourchette motrice est perpendiculaire au plan du joint et
ω1 est la vitesse instantanée d’entrée, ω2 la vitesse de sortie, θ1 l’angle de rotation de l’arbreβ
Si
est l’angle du joint mesuré dans le plan contenant les arbres.T2 est constant comme ω1 T1 = ω2 T2, en négligeant les pertes, on peut exprimer T1 en fonction GD' = HD" et que OG = OH cos β sur la figure 10.21a, on en déduit que :θ2=cos β tan θ1ω1 est connue et c’est le couple deT2 qui dicte la puissance à l’entrée. En dérivant l’expression (10.6) par rapport au temps et enω1 constant, on trouve après simplification que la vitesse de sortie vaut :Le couple à l’entrée varie donc de la même façon que la vitesse de sortie en fonction de la charge.
Dans l’équation (10.7), lorsque
θ1 vaut 0o, on a :ω = ω
Après une rotation de 90C’est dire qu'après une rotation de 90
d’une vitesse plus lente que celle de l’arbre d’entrée à une vitesse plus élevée; il y a donc une
position intermédiaire où Pour des valeurs de
β qui varient de 0o jusqu’à 20o, l’angle θ1 pour lequel ω2 = ω1 se situe entre 44oet 45Si on dérive l’équation (10.7) encore une fois par rapport au temps, on obtient l’accélération
angulaire que subit l’arbre de sortie pour une vitesse de rotation constante de l’arbre d'entrée, soit :L’amplitude de vibration est la différence entre
lorsque pour
θ2 - θ1 s’écrit
Les équations (10.7) à (10.14) décrivent des relations qui donnent la rotation, la vitesse et
l’accélération d’un joint universel. D’une façon plus pratique, si l’angle
équations peuvent être remplacées par les approximations suivantes :où
A et β sont en radians. Ces expressions sont dérivées en détail à la référence [10.5].β est plus petit que 10o, cesθ2 et θ1 sur un tour complet des arbres, c’est-à-direθ1 qui varie de 0 à 360o. On obtiento.o de l’arbre d’entrée, l’arbre de sortie a vu sa vitesse passerω2 = ω1. Ceci se produit pour un angle θ1 donné parcos β 2 1 (10.9)o de l’arbre d’entrée, θ1 = 90o, et l’équation (10.7) donne :θ2 dont a tourné l’arbre de sortie, il faut projeter le point D' sur le cercle en D".θ2 dont a tourné l’arbre de sortie est alors l’angle DOD".GOD' et HOD", on peut écrire :
∠ θ1 de l’arbre d’entrée, l’extrémité B de la croix dans la fourchette deθ1, l’extrémité DBOD se projetter = OB = OC où r est le rayon des bras de la croix. Par contre,θ1. Lorsque θ1 devient compris entre 90o et 180o, l’angle θ2 rattrape son retard et ainsi