Dans les éléments de machines, on cherche habituellement à limiter les déformations. Ceci n’est
pas le cas pour les ressorts, qui sont conçus pour se déformer de façon importante tout en restant
dans le domaine élastique. On introduit à la Figure 7.1 la notion de rigidité, encore appelée
« constante de raideur » dans le domaine élastique linéaire, pour évaluer cette aptitude
particulière.
exercer des forces de rappel pour maintenir des pièces en contact (ressorts de soupape absorber les chocs (ressorts de suspension automobile); emmagasiner et restituer de l’énergie (ressorts de montre, mécanismes déclencheurs); exercer une force (actuateur);
Association de 3 ressorts en série
La force est constante dans les ressorts 1, 2 et 3 (équilibre des forces en statique). On observe
alors les déflections suivantes dans chacun des ressorts :
Par conséquent, la déflection totale y devient 
Nous nous intéresserons dans un premier temps aux ressorts à section circulaire. La
nomenclature qui sera employée est détaillée à la Figure 7.13.
diamètre d’enroulement moyen, rayon d’enroulement, diamètre du fil du ressort, rayon du fil du ressort, 0 = D+d diamètre extérieur, i = D-d diamètre intérieur,
p
pas du ressort, α
=arctan(p/D) angle du ressort, F
force axiale exercée,N Contrainte
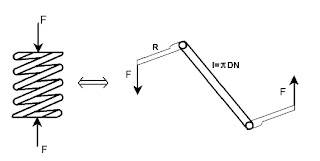
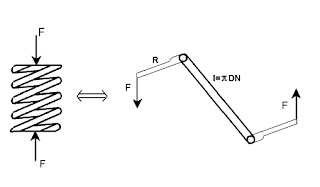
Lorsque l’on comprime le ressort avec une force
ressort est essentiellement de torsion, avec une partie de cisaillement pur. Dans un premier
temps, on ne considère que la torsion, effet principal, notamment pour des ressorts ayant de
grands indices
soumise à un couple de torsion
F, la contrainte engendrée dans une section duD/d et de faibles angles. On assimile ainsi le ressort à une barre cylindrique droiteT s’exprimant comme suit :T= F 
La contrainte de torsion vaut :
On peut raffiner ce modèle en ajoutant les effets du cisaillement, dus à l’éloignement du fil (où
s’applique la charge) à l’axe neutre du ressort. Pour une sollicitation statique, la contrainte
induite à la fibre intérieure s’écrit (Wahl, 1963) :
où
uniquement compte de la torsion et du cisaillementSi l’on veut prendre en compte aussi l’effet de la courbure du fil (effet dynamique), l’expression
de la contrainte se modifie légèrement et prend la forme suivante :
avec les notations :
K
facteur de Wahl (K = Ks Kc ), K
s facteur de correction du cisaillement direct, K
Le paramètre
hélicoïdal cylindrique. Ce facteur de correction dépend de la géométrie du fil du ressort (ici, fil
circulaire), car il intègre les effets de la courbure du fil. En réalité on peut considérer que ce
facteur est le produit de deux effets : la superposition du cisaillement direct à l’effet de torsion
pure (
dans le cas d’un fil circulaire avec la formule suivante :
On note que l’effort maximal sera supporté par les fibres externes situées à l’intérieur du ressort
(vers l’axe du ressort).
a) Théorème de Castigliano
On va à présent calculer le déplacement du ressort (plus particulièrement au point d’application
de la force
élastique, le déplacement correspondant à une force est obtenu en prenant la dérivée partielle de
l’énergie de déformation par rapport à cette force.
Or l’affaissement du ressort hélicoïdal est uniquement dû à la torsion. Il faut donc dériver
l’énergie de torsion 
où
cisaillement dans le plan et
précédemment que le moment de torsion 
Si l’angle
s’exprimer en première approximation sous la forme suivante :
KS est le facteur de correction statique, pour un ressort hélicoïdal cylindrique, qui tientC (C=D/d), on obtient l’expression suivante de la contrainte :A est la section droite du ressort :⋅ D/2 = F ⋅ Rn On obtient finalement :
Donc, en dérivant, il vient :
L’expression de la constante de raideur dérive immédiatement de l’équation (7.13)
F) au moyen du théorème de Castigliano. Celui-ci postule que dans un système
d
•
Du point de vue historique, il convient de considérer comme ressort « tout organe élastique
pouvant supporter d’importantes déformations et destiné à exercer une force en tendant à
reprendre sa forme initiale après avoir été plié, tendu, comprimé ou tordu » d’après la définition
du Petit Larousse. L’idée d’utiliser l’élasticité des matériaux remonte à plusieurs siècles. La
première utilisation répandue de l’effet de rappel du ressort est l’arc. Une évolution significativeAssociation de 3 ressorts en série
apparaît au XI
ressort est ensuite utilisé dans les montres et horloges (pour fournir de l’énergie).
L’invention du ressort hélicoïdal permit d’emmagasiner une plus grande quantité d’énergie dans
un espace plus restreint. Son développement est lié au progrès industriel du XIX
utilisations se diversifièrent au XX
systèmes mécaniques et des domaines variés (automobile, aéronautique…).
Actuellement la limite d’élasticité des matériaux usuels est de 0.15% de déformation. Ainsi il
s’avère nécessaire d’avoir recours à des structures spéciales pour absorber de grandes
déformations tout en restant dans le domaine élastique. On distingue principalement 3 formes de
ressorts: les ressorts cylindriques, coniques et plats. Notons qu’on peut également classer les
ressorts suivant le type de contraintes qu’ils subissent (traction/compression, flexion et torsion).Ressorts plats (à lame)
On va à présent calculer le déplacement du ressort (plus particulièrement au point d’application
de la force
élastique, le déplacement correspondant à une force est obtenu en prenant la dérivée partielle de
l’énergie de déformation par rapport à cette force.
r
Or l’affaissement du ressort hélicoïdal est uniquement dû à la torsion. Il faut donc dériver
l’énergie de torsion 
Deux types de ressorts se dégagent dans cette catégorie. Tout d’abord les ressorts à lame,
sollicités en flexion. Ils peuvent être composés d’une ou plusieurs couches. Ces ressorts, qui sont
notamment utilisés dans les suspensions automobiles, sont constitués de matériaux performants
en flexion, comme l’acier par exemple.
Ressort spiral
Ressorts cylindriques hélicoïdaux
Ils peuvent être utilisés, selon les cas, en compression, tension ou torsion. Leur fil peut être rond,
carré, rectangulaire ou même sous forme de bande.
(a) ressort cylindriques à fil carré et (b) à fil rectangulaire
Ce type de ressort est devenu très populaire, au point qu’il est associé à la notion même de
ressort dans l’esprit des gens. Le plus généralement, ces ressorts sont sollicités en torsion, par
l’action d’une force axiale visant à les comprimer La démonstration en sera
établie ultérieurement.
Compression d’un ressort hélicoïdal cylindrique,
induisant une contrainte de torsionOn note cependant des applications où le ressort est sollicité en flexion : il s’agit par exemple
d’un ressort créant un couple de torsion pour maintenir l’écartement entre deux pièces reliées par
une liaison pivot (comme dans une agrafeuse par exemple).
Ressorts coniques hélicoïdaux
On trouve également des ressorts hélicoïdaux dont le rayon d’enroulement est variable, ce qui
donne une forme conique au ressort. Ceux-ci ont l’aptitude, une fois comprimés, de s’enrouler
sur eux-mêmes, augmentant par-là même leur déflection maximale (alors qu’elle est limitée par
la butée des spires l’une sur l’autre dans le cas d’un ressort cylindrique). En outre, on observe
que la raideur de ce type de structure croît avec la déflection imposée. Les ressorts coniques sont
utilisés entre autres dans les matelas.Ressorts à disque (rondelles « Belleville »)
Les ressorts Belleville sont formés de disques circulaires courbés à leur extrémité. Ils sont
caractérisés par l’épaisseur du disque
généralement lorsque l’espace est très restreint dans la direction du chargement, ou quand on
souhaite une réponse charge-déformation non linéaire.La constante de raideur k d’un ressort est définie comme suit
où
force au point d’application (m ou po). La constante de raideur s’exprime en N/m.
Réponse d’un ressort hélicoïdal à un chargement axial
On observe différents types de réponse selon la structure du ressort et le mode de sollicitation.
On peut observer 3 types de réponse à la Figure 7.8 : réponse progressive, linéaire et dégressive.
Egénéral, la valeur de k est constante pour un ressort donné, c’est-àque la force est
directement proportionnelle à la déflection : la réponse du ressort est alors linéaire.n -dire 
Dans le cas d’un ressort à déformation angulaire (ressort de torsion), on définit de façon
analogue la constante de raideur comme 
où
Abordons maintenant la capacité d’un ressort à emmagasiner de l’énergie sous forme élastique.
Les énergies potentielles de déformation en tension et en torsion par unité de volume s’expriment
comme suit :
où
contrainte de cisaillement engendrée dans le matériau du ressort. Ces formules sont valables
lorsque les contraintes sont distribuées uniformément. Sinon il faut avoir recours à un facteur de
Ainsi, pour les ressorts hélicoïdaux, ce facteur vaut 1/2
introduit plus loin). L’énergie potentielle élastique emmagasinée dans un ressort de torsion
s’écrit donc : 
On peut calculer l’énergie élastique d’un ressort d’une autre manière, en exprimant le travail
accompli par la force 
On peut associer les ressorts en parallèle de différentes manières. Tout d’abord, examinons le cas
le plus répandu où chaque ressort a la même longueur libre
On calcule la raideur équivalente pour ce système de ressorts. Tout d’abord la charge se répartit
sur les 3 ressorts, soit :
La constante de raideur équivalente
On obtient ainsi une réponse charge-déflection qui est linéaire par morceaux :
On peut également associer les ressorts en série :
La force est constante dans les ressorts 1, 2 et 3 (équilibre des forces en statique). On observe
alors les déflections suivantes dans chacun des ressorts :R
Nous nous intéresserons dans un premier temps aux ressorts à section circulaire. La
nomenclature qui sera employée est détaillée à la Figure 7.13.
Les paramètres géométriques d’un ressort hélicoïdal cylindrique (cf. Figure 7.13) sont notés
comme suit :D
diamètre d’enroulement moyen, R
rayon d’enroulement, d
diamètre du fil du ressort, r
rayon du fil du ressort, D
0 = D+d diamètre extérieur, D
i = D-d diamètre intérieur, p
pas du ressort, α
=arctan(p/D) angle du ressort, F
force axiale exercée,N Contrainte
Lorsque l’on comprime le ressort avec une force
ressort est essentiellement de torsion, avec une partie de cisaillement pur. Dans un premier
temps, on ne considère que la torsion, effet principal, notamment pour des ressorts ayant de
grands indices
soumise à un couple de torsion
F, la contrainte engendrée dans une section duD/d et de faibles angles. On assimile ainsi le ressort à une barre cylindrique droiteT s’exprimant comme suit :T= F 
Modélisation d’un ressort hélicoïdal en barre de torsion
La contrainte de torsion vaut :
On peut raffiner ce modèle en ajoutant les effets du cisaillement, dus à l’éloignement du fil (où
s’applique la charge) à l’axe neutre du ressort. Pour une sollicitation statique, la contrainte
induite à la fibre intérieure s’écrit (Wahl, 1963) :
C (C=D/d), on obtient l’expression suivante de la contrainte :A est la section droite du ressort :τ est donné ici par la formule⋅ D/2 = F ⋅ Rnombre de spires.
Il existe également les ressorts en spirales, dont la fonction est d’exercer un couple de torsion de
rappel (par exemple dans le mécanisme des montres).
où
cisaillement dans le plan et
précédemment que le moment de torsion 
Si l’angle
s’exprimer en première approximation sous la forme suivante
On présente une autre méthode de calcul de la déflection axiale, plus conventionnelle. On
considère le ressort comme une barre droite, dont la déflection sera uniquement due à la torsion.
On a appliqué le même couple T, ainsi en déroulant le ressort on obtient l’angle total de rotation :α est faible et N désigne le nombre de spires du ressort, la longueur du fil peutD
